What Does Ø Mean In Math
douglasnets
Nov 28, 2025 · 14 min read
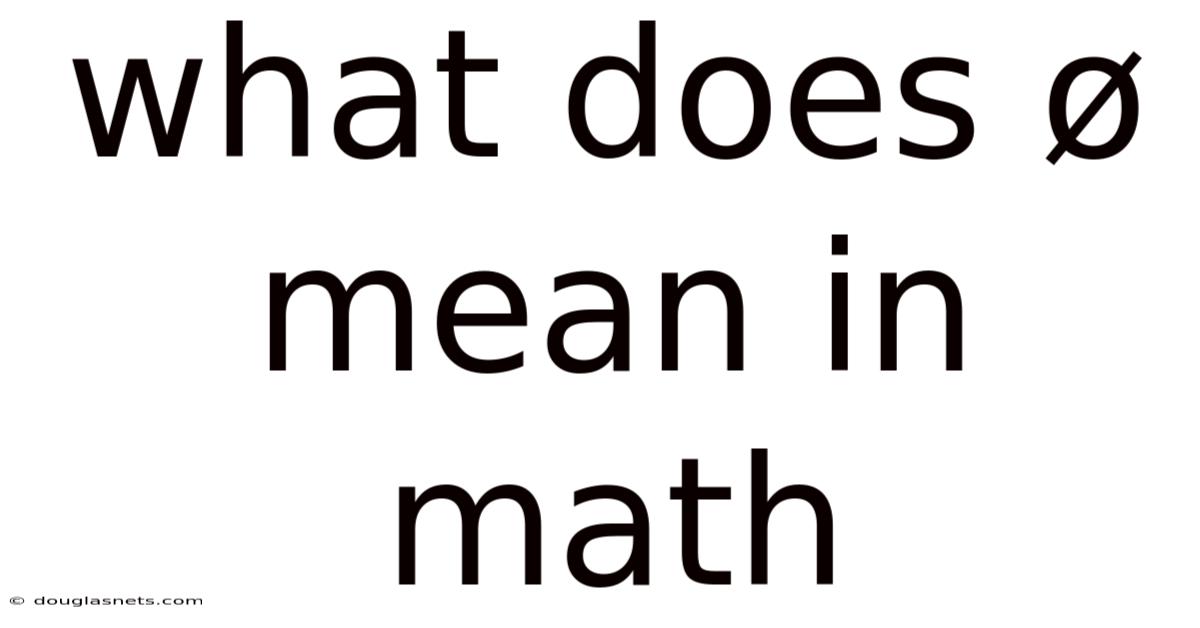
Table of Contents
Have you ever stumbled upon a symbol in a math equation that looks like a slashed zero? It might have appeared in a set theory problem or perhaps while exploring concepts in abstract algebra. This symbol, "ø," is more than just a zero with a line through it; it represents a profound concept in mathematics: the null set or empty set. Understanding what the null set signifies is crucial for mastering various branches of mathematics, from basic set operations to advanced topics in topology and analysis.
The null set, denoted by "ø" or "{}", is a set containing no elements. It's a fundamental concept in set theory, acting as a mathematical void. Imagine a box that's completely empty – that's essentially what the null set is. Despite its emptiness, it plays a crucial role in the logical structure of mathematics. Without it, many set operations and mathematical definitions would become inconsistent or incomplete. In this article, we’ll explore the comprehensive aspects of the null set, understand its properties, and discover how it is applied across different mathematical disciplines.
Main Subheading
The concept of the null set emerged from the formalization of set theory in the late 19th and early 20th centuries. Before set theory was rigorously defined, mathematicians often struggled with paradoxes and inconsistencies that arose from dealing with infinite sets and undefined collections. Georg Cantor, a pioneer in set theory, laid the groundwork for understanding sets of various sizes, including infinite sets. However, the formal definition of a set and the operations that could be performed on sets required a clear understanding of what constituted a set, even if it contained nothing.
The formal introduction of the null set helped to resolve many of these inconsistencies. It provided a base case for defining set operations and relations. For example, the intersection of two disjoint sets (sets with no common elements) is the null set. Without the null set, this operation would be undefined, leading to logical problems. The null set also serves as the identity element for certain set operations, such as the union operation on sets of a particular algebra. Its inclusion ensured that set theory could be developed on a solid foundation, free from contradictions.
Comprehensive Overview
Definition and Basic Properties
The null set, also known as the empty set, is uniquely defined as the set containing no elements. Formally, it can be defined using predicate logic as follows:
ø = {x | x ≠ x}
This notation reads as "the set of all x such that x is not equal to x." Since there is no element that satisfies this condition, the set is empty.
Key properties of the null set include:
- Uniqueness: There is only one null set. Any set with no elements is the null set.
- Subset of Every Set: The null set is a subset of every set. This means that for any set A, ø ⊆ A. This property can be proved by contradiction. Suppose ø is not a subset of A. Then there must exist an element x in ø such that x is not in A. But ø has no elements, leading to a contradiction. Therefore, ø must be a subset of A.
- Intersection Property: The intersection of any set A with the null set is the null set: A ∩ ø = ø. This is because the intersection of two sets contains only the elements that are in both sets. Since the null set has no elements, there can be no common elements between A and ø.
- Union Property: The union of any set A with the null set is the set A itself: A ∪ ø = A. This is because the union of two sets contains all the elements that are in either set. Adding the null set, which has no elements, does not change the elements in A.
- Cardinality: The cardinality (number of elements) of the null set is zero: |ø| = 0.
Scientific Foundations
The scientific foundation of the null set lies in the axiomatic construction of set theory. Zermelo-Fraenkel set theory (ZFC), which is the most widely accepted axiomatic system for set theory, includes axioms that ensure the existence and properties of the null set. Specifically, the axiom of the empty set states that there exists a set with no elements. From this axiom, the null set can be uniquely defined and its properties can be derived using the other axioms of ZFC.
The role of the null set is pivotal in constructing more complex mathematical structures. For instance, the natural numbers can be defined using set theory, starting with the null set. In this construction, 0 is defined as the null set, and each subsequent natural number is defined as the set containing all the preceding natural numbers. This approach provides a rigorous foundation for arithmetic and number theory.
Historical Context
The historical development of the null set is closely tied to the formalization of set theory in the late 19th and early 20th centuries. Georg Cantor's work on infinite sets and the development of set theory by mathematicians such as Richard Dedekind and Ernst Zermelo highlighted the need for a precise definition of sets and set operations. The introduction of the null set was a crucial step in this formalization process.
Giuseppe Peano, an Italian mathematician, was among the first to explicitly use a symbol to represent the empty set in his work on the foundations of mathematics. However, the notation "ø" became widely adopted due to its use in the Bourbaki series, a comprehensive and influential series of books on mathematics written by a group of mostly French mathematicians under the pseudonym Nicolas Bourbaki.
Applications in Different Fields
The null set finds applications in various branches of mathematics and computer science. Here are a few examples:
- Set Theory: As previously mentioned, the null set is a fundamental concept in set theory. It is used to define set operations, relations, and functions.
- Logic: In mathematical logic, the null set can represent a contradiction or an impossible condition. For example, if a statement leads to the conclusion that an element belongs to the null set, then the statement is false.
- Probability Theory: In probability theory, the null set represents an impossible event. The probability of the null set is zero, indicating that the event will never occur.
- Topology: In topology, the null set is both open and closed. This property is essential for defining topological spaces and continuous functions.
- Computer Science: In computer science, the null set is used in the theory of formal languages and automata. For example, a finite automaton may have a transition that leads to the null set, indicating that the automaton cannot accept certain input strings.
- Database Management: In database management, a query that returns no results can be thought of as returning the null set. This is an important concept for handling queries and data manipulation.
Common Misconceptions
There are several common misconceptions about the null set that often lead to confusion. Understanding these misconceptions is crucial for a clear grasp of the concept.
- The Null Set is Not the Same as Zero: While the cardinality of the null set is zero, the null set itself is not the same as the number zero. The null set is a set with no elements, whereas zero is a number representing the absence of quantity.
- The Null Set is Not the Same as a Set Containing Zero: The set {0} is not the null set. The set {0} contains one element, namely the number zero. The null set contains no elements.
- The Null Set is Not Undefined: The null set is a well-defined concept in mathematics. It is uniquely defined as the set containing no elements.
- The Null Set is Not Insignificant: Despite being empty, the null set plays a significant role in the logical structure of mathematics. It is essential for defining set operations, relations, and functions.
Trends and Latest Developments
While the concept of the null set is well-established, its applications and interpretations continue to evolve alongside advancements in mathematical research and related fields. Here are some current trends and developments:
Formal Verification
In computer science and software engineering, formal verification techniques are used to prove the correctness of algorithms and software systems. The null set plays a role in these techniques, particularly in the context of model checking and automated theorem proving. For example, if a formal specification requires a set of conditions to be met, and it can be shown that no such conditions exist (i.e., the set of conditions is the null set), then the system is considered safe with respect to that specification.
Category Theory
Category theory is a branch of mathematics that studies abstract structures and relationships between them. In category theory, the null set (or initial object) is a fundamental concept. It serves as the starting point for constructing more complex objects and morphisms. Category theory provides a powerful framework for unifying different areas of mathematics and computer science, and the null set plays a crucial role in this framework.
Quantum Set Theory
Quantum set theory is an emerging field that combines quantum mechanics with set theory. In this framework, sets can exist in superposition, meaning that an element can be partially in a set and partially not in a set. The null set in quantum set theory is not simply an empty set but can have quantum properties, leading to new mathematical structures and potential applications in quantum computing and information theory.
Data Science and Machine Learning
In data science and machine learning, the null set can appear in various contexts, such as feature selection and data preprocessing. For example, if a feature in a dataset has no variance (i.e., all values are the same), it can be considered to belong to a null set of informative features and may be removed from the dataset to improve model performance. Similarly, in clustering algorithms, a cluster that contains no data points can be considered a null set.
Professional Insights
From a professional perspective, understanding the null set is not just an academic exercise but a practical skill that can be applied in various domains. For instance, in software development, being able to recognize and handle edge cases where a set of data is empty can prevent errors and improve the robustness of software systems. In data analysis, understanding how to interpret and handle null sets in data can lead to more accurate and reliable results.
Tips and Expert Advice
To master the concept of the null set, consider the following tips and expert advice:
1. Practice Set Operations
The best way to understand the null set is to practice set operations involving the null set. Work through examples of unions, intersections, and complements of sets, including the null set. This will help you internalize the properties of the null set and how it interacts with other sets.
For example, consider the following sets: A = {1, 2, 3}, B = {3, 4, 5}. Then:
- A ∪ ø = {1, 2, 3}
- A ∩ ø = ø
- (A ∪ B) ∩ ø = ø
2. Understand the Axiomatic Foundation
To gain a deeper understanding of the null set, study the axiomatic foundation of set theory, particularly the Zermelo-Fraenkel axioms. Understanding how the null set is defined and its properties are derived from these axioms will give you a solid theoretical foundation.
3. Visualize Sets
Visualizing sets using Venn diagrams can be helpful for understanding set operations involving the null set. Draw Venn diagrams for different sets and shade the regions corresponding to unions, intersections, and complements. This will help you see how the null set behaves in relation to other sets.
For example, if you have a set A and you want to visualize A ∩ ø, you will see that there is no overlap between A and the null set, illustrating that the intersection is empty.
4. Apply the Concept in Different Contexts
The null set appears in various branches of mathematics and computer science. Try to apply the concept in different contexts to deepen your understanding. For example, consider how the null set is used in logic, probability theory, topology, and computer science.
For example, in probability theory, the null set represents an impossible event. Understanding this connection can help you solve probability problems more effectively.
5. Avoid Common Mistakes
Be aware of the common misconceptions about the null set. Remember that the null set is not the same as zero, it is not the same as a set containing zero, and it is not undefined. Keeping these distinctions in mind will help you avoid confusion and errors.
6. Explore Advanced Topics
Once you have a solid understanding of the basic properties of the null set, explore advanced topics that build on this concept. For example, study category theory, quantum set theory, or formal verification techniques. These topics will give you a broader perspective on the role of the null set in mathematics and related fields.
7. Teach Others
One of the best ways to master a concept is to teach it to others. Try explaining the null set to a friend or colleague. This will force you to organize your thoughts and articulate the concept clearly, which will solidify your own understanding.
8. Use Online Resources
There are many online resources available that can help you learn more about the null set. Explore websites like Khan Academy, Wolfram MathWorld, and Wikipedia. These resources provide definitions, examples, and exercises that can help you deepen your understanding.
9. Solve Problems Regularly
Regularly solving problems that involve the null set is essential for mastering the concept. Work through exercises in textbooks, online problem sets, and past exams. The more you practice, the more comfortable you will become with the null set and its applications.
10. Seek Expert Guidance
If you are struggling to understand the null set, don't hesitate to seek guidance from a mathematics professor, tutor, or expert. They can provide personalized explanations and help you overcome any difficulties you may be facing.
FAQ
Q: What is the difference between the null set and the universal set?
A: The null set is a set containing no elements, while the universal set is a set containing all possible elements under consideration. The null set is a subset of every set, while every set is a subset of the universal set.
Q: Is the null set finite or infinite?
A: The null set is finite. Its cardinality (number of elements) is zero, which is a finite number.
Q: Can a set contain the null set as an element?
A: Yes, a set can contain the null set as an element. For example, the set {ø} contains one element, which is the null set. This set is different from the null set itself, which contains no elements.
Q: How is the null set used in computer science?
A: In computer science, the null set is used in various contexts, such as the theory of formal languages and automata, database management, and algorithm design. It represents an empty set of data or a condition that cannot be satisfied.
Q: Why is it important to understand the concept of the null set?
A: Understanding the concept of the null set is important because it is a fundamental concept in set theory and plays a crucial role in the logical structure of mathematics. It is used to define set operations, relations, and functions, and it appears in various branches of mathematics and computer science.
Conclusion
In summary, the null set (ø) is a fundamental concept in mathematics, representing a set with no elements. Despite its apparent simplicity, it is crucial for defining set operations, ensuring logical consistency, and providing a foundation for more complex mathematical structures. Understanding the properties of the null set, its applications in various fields, and common misconceptions surrounding it, is essential for any student or professional in mathematics, computer science, or related disciplines.
We encourage you to delve deeper into the world of set theory and explore how the null set underpins many advanced mathematical concepts. To further your understanding, try working through exercises involving set operations and exploring the axiomatic foundations of set theory. Share this article with your peers and discuss how the concept of the null set applies in your respective fields. By engaging with this topic and applying it in practical contexts, you can gain a more profound appreciation for its significance and utility.
Latest Posts
Latest Posts
-
How To Turn In A Snowboard
Nov 28, 2025
-
Anime Characters With Red And White Hair
Nov 28, 2025
-
How To Remove Chewing Gum Stain
Nov 28, 2025
-
How To Use An Electric Lighter
Nov 28, 2025
-
Do Kiwis Need To Be Organic
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Does Ø Mean In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.